平面の等量等形分割『凸５角形（ガイドあり）』

――　まえがき　――
１種類の図形を使用して、平面を等量等形分割する方法について解説します．

最終的に使用する図形は凸５角形ですが、途中まで等辺凸６角形をガイドとして使用します．

基本図形、ガイド図形、作図方法、タイル張り手順、応用作品例を提示します．

――　ギャラリー１　――

――　ギャラリー２　――

――　基本図形　――
凸５角形の内角と辺は下記の通りとします．

内角：７２度、１４４度、１４４度、９０度、９０度
辺の長さの比率： 1 対 1 対 0.5 対 0.5 対 1.17557

――　ガイド図形　――
等辺凸６角形の内角と辺は下記の通りとします．

内角：７２度、１４４度、１４４度、７２度、１４４度、１４４度
辺：すべて同じ長さ

――　作図方法　――
まず正１０角形を考えます．

正１０角形の外周のうち、連続する３辺を選びます．そして、この３辺を内側へ折り返します．選んだ外周の３辺と内側に折り返した３辺に囲まれた図形がガイド図形の等辺凸６角形です．

この等辺凸６角形を二等分したものが凸5角形です．逆の言い方をすると、凸５角形をふたつ組み合わせたものが等辺凸６角形です．

タイル張り手順では、ガイド図形の等辺凸６角形を使用して、二回回転対称性のあるタイル張りを示します．その後に、等辺凸６角形を二等分して、基本図形の凸５角形によるタイル張りを完成します．

――　タイル張り手順１　――
まず、等辺凸６角形を６個用意して図のように組み合わせます．

――　タイル張り手順２　――
等辺凸６角形の１４４度の頂点と別の１４４度の頂点が重なった所では、７２度の空ができます．

３６０° － ２ ｘ １４４° ＝ ７２°

この空に、等辺凸６角形の７２度の頂点を差し込みます．

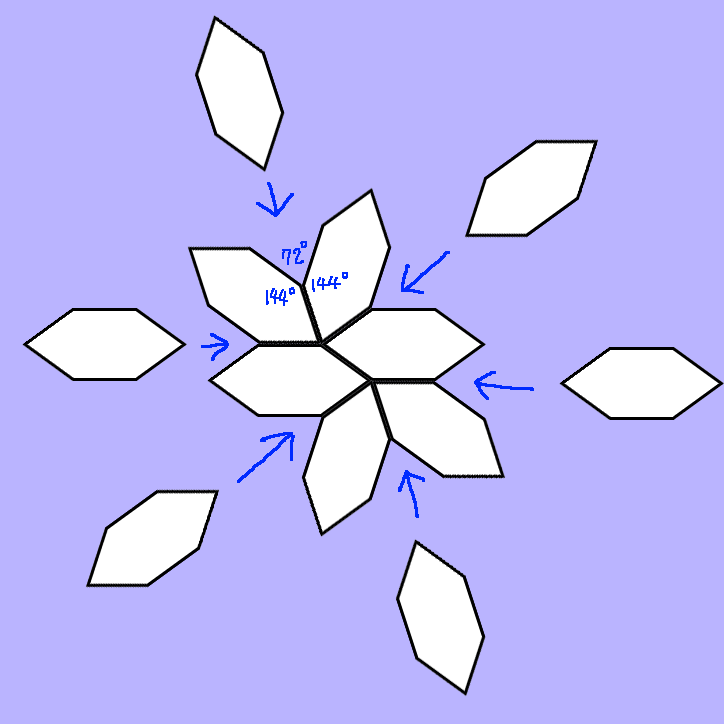
――　タイル張り手順３　――
７２度の空に、次々と等辺凸６角形の７２度の頂点を差し込んで行きます．

――　タイル張り手順４　――
無限にタイル張りを続ける事が出来て、２回回転対称になると思います．
（証明は行なっておりません）

――　タイル張り手順５　――
等辺凸６角形をふたつの凸５角形で置き換えます．

凸５角形による平面の等量等形分割の完成です．
（了）

――　あとがき　――
この本はパブーに於いて公開している電子書籍、エッセイ（数学）『平面の等量等形分割（凸５角形）』を加筆修正したものです．